
Neural networks are popular. A quick search on Arxiv for ‘neural network’ in the abstract of its database of research papers yields about 15,000 results. By comparison, searching for the term ‘regression’ only produces just short of 8,800 results and this term encompasses the popular linear/logisitc regression method, which are prerequisites to neural network theory. Even ‘hydrogen’ has less abstract hits than ‘neural network’! That is why, for your deep-learning desires, I have procured another article about neural networks to toss into the compost of backprop and brains and the end of humanity as we know it. I hope this one will be a little different from the rest. By starting from basic principles of neural networks and the simple multilayer perceptron, the neural network will be developed in a new light. This perspective of neural networks is not novel (see similar concepts such as cellular neural networks, smooth life, and lenia), but it hasn’t garnered much attention. Some wrangle with machine learning from a dense statistical basis. Others wield the mighty physics and cast fascinating insight through thermodynamics and particle theory. I have a diposition to draw upon biology and nature; the great tinkerer. Much of what humanity has created throughout history was either influenced by nature or we later found out that evolution beat us to the discovery.
A Simple Model of Life
Those with a computer science background will have programmed Conway’s Game of Life. I hesitate to introduce cellular automata in this cliché manner, but it stands that Game of Life, or GoL, sparked a revolution in the field of reproducing machines, artificial life, and generative art. Conway conceived of GoL when he was trying to develop a simulation for biological life which required few rules. He managed it in four. Conway’s world was a grid, where each cell is either ON or OFF. In this world time moves forward in discrete steps, and every cell updates synchronously based on a ruleset. A rule in the ruleset is just an output of a function, whos input is the cell’s neighbours. Conway created these four rules:
- ) If a cell has 3 ON neighbours and is OFF, turn ON.
- ) If a cell has more than 3 ON neighbours, turn OFF.
- ) If a cell has 2 or 3 neighbours and is ON, stay ON.
- ) If a cell has fewer than 2 neighbours, turn OFF.
Some intricate and unforseable patterns can emerge from the simple dynamics. Below is a spaceship, a moving constant body within the GoL universe. It is active research within the GoL community what the limits of the spaceships are.
Conway’s life model is a cellular automata. These minimal models were first developed collaboratively by Von Nuemann and Stanislaw Ulam. By asking the question of whether a program could reproduce, together Von Nuemann and Ulam devised a simple discrete two-dimensional lattice-based model which could create copies of itself. Since the 1940s, the principles governing cellular automata have become more generalised, leading to interesting microbial-like worlds. Some interesting variations include sexyloop, smooth life, Langston’s ant, and Subset Sum Automata. First, I will define the mathematics which describe cellular automata. Then, from these definitions I will show you how cellular automata, with a few generalisations, are equivalent to a model of neural networks.
From Cellular Automata to the Brain
Traditionally, cellular automata are based on a $d$ -dimensional lattice $\mathbb{R}^d$ . The lattice can be generalised as a cyclic graph $G=\{N,W\}$ where
$N=\{n_{i,t} | i \in \mathbb{R}, t \in \mathbb{N} \}$
is the set of cells and
$W=\{w_{i,j} \in \{0,1\} | i,j\in|N|\times|N|\}$
is the set of edges for edge $(i,j)$. Therefore the classic two-dimensional finite lattice of size $|N^{1/2}|\times|N^{1/2}|$ which Game of Life uses can be described by $w_{i,i-1}=1$ , $w_{i,i+1}=1$ , $w_{i,i+|N^{1/2}|}=1$ , $w_{i,i-|N^{1/2}|}=1$ for $i=0…N-1$ , $w_{i,k}=0$ otherwise. I have taken liberties and removed the $(\cdot)mod|N^{1/2}|$ around each increment of $i$, but this should be included to allow the graph to wrap around infinitely. A cellular automata has a rule function defining how a cell’s state $n_{i,t-1}$ changes at time $t$ given time $t-1$:
$n_{i,t+1}=r(n_{i,t}, c(n_{i,t}))$
where $n_{i,t}$ is the state of cell $i$ at time $t$ and $c(n_{i,t})$ are the neighbours of cell $i$ at time $t$, where a neighbour of a node is another node connected to it by an edge. For the two-dimensional case, the neighbours are
$c(n_{i,t})=\{n_{i+1,t},n_{i-1,t},n_{i-|N^{1/2}|,t},n_{i+|N^{1/2}|, t}\}$.
A rule can be homogeneous, meaning that every cell has the same rule, or heterogeneous, meaning that cells may each have their own rules, denoted $r_{i,t}(\cdot)$. At each timestep, all cells states are updates synchronously - of course this can be generalised to the asynchronous updates - by applying the rule function to each cell.
For simplicity, we will create a single-hidden-layer feedforward neural network from cellular automata principles, but this can intuitively be generalised to more layers and recurrent connections. Even more interesting would be to explore how this translates to convolutional models. I’ll leave this as a later exercise. The first step is to devise a ‘lattice’ for our cellular automata which reflects a neural network architecture. We are only intrested in the topology of the feed-forward neural network right now, therefore our graph will not be weighted. Our neural network will consist of $|I|$ input nodes, $|H|$ hidden nodes and $|O|$ output nodes. The cellular automata graph is therefore $G=\{I \cup H \cup O,W\}$ where $I,H,O$ are the sets of nodes and $W$ are the edges. We apply two constraints to the edges:
- Edges which exist between layers - e.g. from layer $I$ to $H$ or $H$ to $O$ but not $I$ to $O$ - have value $w_{i,j} = 1$. Otherwise $w_{i,j} = 0$. There are no recurrent weights, that is, $w_{i,i}=0$.
- Edges can only go forward. Based on the first constraint, if $w_{i,j} \in 1$ then $w_{j,i} = 0$.
This is described by the constraint $w_{i,j} = 1$ for $\{(i,j \in |I|\times|H|), (i,j \in |H|\times|O|)\}$ else $w(.,.)=0$. Our cellular automata graph now represents an topologically-identical graph to a feedforward neural network, but it will not behave like a neural network yet. Neural networks use a weighted sum of inputs along with an activation function to non-linearly transform data as it moves through the graph. Naturally, this activation function can be represented via the cellular automata rule $r(\cdot)$. It may have seemed counter intuitive to not incorporate the weight values into the edges of the cellular automata graph and use these as information passes between nodes. The problem is, by making this decision we would deviate from the original cellular automata structure defined earlier, where a cell’s state is updated purely based on its neighbours’ states. Instead, the weight information is kept inside each cell as a unique rule. The figure below illustrates this concept.
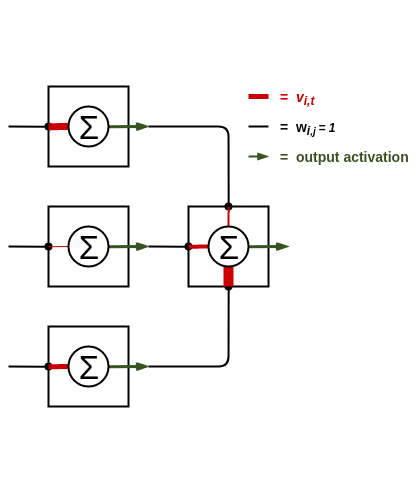
Figure 1: Three cells feed their inputs into a fourth cell in a higher layer. Note that the black connections indicate the graph topology such that they are all edges of value 1. The weighting of the inputs to the cell are done inside the cell, as denoted by the thickness of the red pathways indicating the scale of the weight.
Each node in a neural network has a unique output based on the weighted sum of its inputs, so each cell in the cellular automata interpretation should have a unique rule. The neural-network cellular automata is therefore heterogeneous in its ruleset. A cell’s heterogeneous rule is defined as:
$r_{i}(n_{i,t}, c(n_{i,t}))=\sigma(\sum_{k \in c(n_{i,t})} v_{i,t}(k)\times k)$
$v_{i,t}(\cdot,\cdot)$ is unqiue for each cell $i$ and is function of the cell’s neighbours. It outputs the input weight from that specific neighbour. That is, each cell stores a list of real values $v_i(k)$ for each neighbour $k$. Instead of updating the cell’s state as a discrete lookup table based on the various permutations of a cell’s neighbours and itself, as is done in Conway’s Game of Life for example, the cell’s state is updated to a real value which is a weighted sum of the state of its neighbours. An activation function $\sigma(\cdot)$ is then applied to this weighted summation, seasoned according to taste.
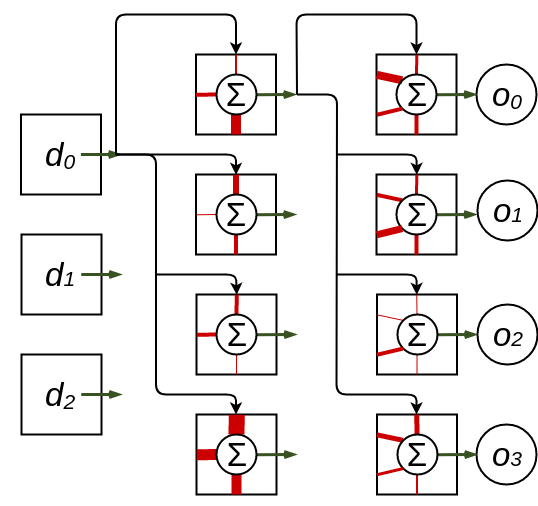
Figure 1: A layout of a one-hidden-layer neural network architecture of a cellular automata. The hidden layer has three inputs and the output layer has four inputs. Note that only the graph connections of the first cell of each layer are drawn to avoid cluttering the diagram. $d_i$ denotes the input data and $o_i$ denotes the output data of the architecture.
This completes the definition of the cellular automata neural network. So how do we use this cellular automata neural network? It is suprisingly straightforward. First, initialise all the cell states to zero. This keeps all cell states at zero even if their state is updated. Then, for each input data vector, assign the input cells the state of that data. That is, for data vector $\vec{d} \in \mathbb{R}^{|I|}$, $n_{i,t}=d_{i}$ where $i$ is in the set of indices for input nodes $I$. To feed the data through to the output, run the cellular automata for one timestep per layer - two timesteps in the case of the single-hidden layer model described above. The output of the neural network is the vector defined by the states of the final output cells: $\vec{o}=(n_{j,t+2},n_{j+1,t+2},…,n_{j+|O|-1,t+2})$. This can be parallelised by feeding data into the input cells at every timestep.
Final Thoughts
Although a fun exercise, the applications for this reformulation are not initially clear. Feedforward neural networks are useful computational tools because the matrix-based model allows for quick forward propagation of the data and parallelisable weight learning. Using this cellular automata interpretation would remove all these speedup advantages.
But, by changing the perspective on the neural network model to that of a cellular automata, it opens up the possibility to apply research in the field of cellular automata to the neural network model. For example, Moshe Sipper introduced a clever way to co-evolve heterogenous cellular automata by using competition between neighbours on a lattice. His paper titled Co-evolving Non-Uniform Cellular Automata to Perform Computations can be found here. An interesting application would be to treat each node in a neural network as a cell with a rule defined by its input weights; nodes compete and crossover to evolve new weight combinations. The fitness of a node could be described in two ways: how much it contributes to the error of the overall objective by using the gradient, or by how much the error changes when the neuron is not present - similar to a VCG auction mechanism. Another use case was alluded to earlier. Asynchrony. Most things, including our brains, are asynchronous because most natural systems are distributed, meaning they use only local interactions to determine how to behave. To my best knowledge, I know of no research into running neural networks asynchronously and what reperecussions that would have to the model. Most likely this is something more applicable to spiking neurons. Nonetheless, the cellular automata version of neural networks would work because each cell internalises its own computation. When a cell is ready to ‘fire’ it observes its neighbour’s states and updates its own state according to its rule function. By the cell’s next firing, its neighbour could have updated twice more! Who cares. To make things interesting, each cell could also have its own update rate $\tau_i \in \mathbb{N}$, which defines the cells period of ‘firing’.
In conclusion, I hope to have heated up your low-temperature simplex thoughts on neural networks. Don’t let your perspectives crystalise too much and remain open to new interpretations.
*In a future post I hope to implement this architecture and explore its properties. Using David Ackley’s Movable Feast Machine written in the language Ulam would be interesting.
The graphic at the top of this post: “Can Cellular Automata Help Us Understand Neural Networks?” via VQGAN+CLIP.