While playing around with shapes today, I asked myself the question of whether information could be encoded in a shape. To simplify the general question, I tried to come up with a result for polygons. Each side of the polygon is a digit in a binary number, and the side may either protrude to represent a one, or remain smooth to represent a zero. I imagined these polygons as boam cutouts being deposited on the surface of water, and wondered what their interactions could ‘compute’. But, before I even began thinking about how these foam polygons would bump on the water, I realised a flaw. As a foam polygon floats, its binary digit will change because the intended Euclidean position of each vertex will rotate. Thus, what would have been an $N$-sided polygon number system with $2^N$ possible numbers, quickly reduced. How much did rotations reduce the maximum number I could represent for an $N$-sided polygon?

My first thought was that this would be a quick combinatorics problem. It soon turned out to be quite tricky. I haven’s found a solution yet, but this is more likely a testament to my rusty maths abilities rather than a the problems difficulty. For those who don’t know the answer, I present some of my work below. For those who do know the answer, we would all love to know.

In the following diagram, I have drawn out all the possible shapes that can be made for polygons of size $N \in {3,4,5,6}$. Heptagons is where my symmetrical doodling abilities curtailed. A red side represents a side with a protrusion. A black side is smooth.

So for $N \in {3,4,5,6}$ the number of possible admissible shapes, $S(N)$, is $S(3)=4$, $S(4)=6$, $S(5)=8$, $S(6)=14$. What I enjoy about the puzzle is that it first appears simple. For example, we can correctly predict $S(3)$ like so. First, we know there is only one case for all sides protruding (+1) and no sides protruding (+1). Second, there must also be only one shape with a single protrusion (+1). Third, the shape with two protrusions has symmetry on either side of the single-protrusion shape, as there are only two sides two choose, there must by only one shape with two protrusions (+1). This results in a total of four admissible shapes for $N=3$. The same line of reasoning works swell for $N=4$ until we encounter the square with the top and bottom protruding. Unlike the ‘ordinary’ shapes before, where four rotations resulted in four unique orientations, this top-bottom protruding square only has two unique orientations. This is diagrammed in the image below.

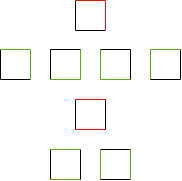
This is particulary tricky because any rule for counting rotations fails. Therefore we need to also know the number of possible symmetries. If we focus on odd-sided polygons for now, we don’t have to deal with the symmetry case. In the odd-sided case we have a solution!

$S(N)=2^N - (N-1)(Z)$

“Wow!”, you might say, that wasn’t so difficult. The above equation makes sense intuitively. There are $2^N$ possible protrusion shapes, irrelevant of rotation. Then, for each possible unique shape that has a protrusion count which is greater than zero but less than $N$, we have $N-1$ rotations we can make. Hence we subtract $N-1$ for each of these admissible shapes. The number of admissibles is $Z$. In the case of a pentagon, $Z=6$. But, disappointingly this solution requires us to know $Z$, which is not so easy.

Below each shape in the first figure, you might have noticed I wrote a binary number ‘barcode’. One method of manipulation that was tried was to permute the binary number by bit-shifting it modulo the maximimum number for the polygon. The puzzle can then be restated as, “Given a length of $N$, how many unique binary digits of length $N$ can be made such that no binay digit is obtainable by another binary digit via bit-shifting modulo $2^N$?”

Hopefully a solution will be with us soon.